基础的算法及相关知识小节
- 算法的性能及大O表示法
- 二分搜索
- 数学归纳法
- 插入排序
- 快速排序
- 归并排序
- 排序性能
- 有向图和无向图
- 图和树的区别
- 前缀表达式,后缀表达式
- 深度优先
- 广度优先
- 最短路径
- KMP算法
- 有限自动机匹配字符串
- 参考
注:本文中内容均来自网络,文末注明了参考过的所有网址,侵删
算法的性能及大O表示法
大O符号(英语:Big O notation)是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。
大O符号在分析算法效率的时候非常有用。举个例子,解决一个规模为\(n\)的问题所花费的时间(或者所需步骤的数目)可以表示为:\(T(n)=4n^2-2n+2\)。当\(n\)增大时,\(n^2\)项将开始占主导地位,而其他各项可以被忽略。举例说明:当\(n=500\),\(4n^2\)项是 \(2n\)项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
进一步看,如果我们与任一其他级的表达式比较,\(n^2\)项的系数也是无关紧要的。例如:一个包含\(n^3\)或\(n^2\)项的表达式,即使 \(T(n)=1,000,000\cdot n^2\),假定 \(U(n)=n^3\),一旦\(n\)增长到大于1,000,000,后者就会一直超越前者(\(T(1,000,000)=1,000,000^3=U(1,000,000)\))。
这样,大O符号就记下剩余的部分,写作:\(T(n)\,{\in}\, \mathcal{O}(n^2)\)或\(T(n)=\mathcal{O}(n^2)\)
并且我们就说该算法具有\(n^2\)阶(平方阶)的时间复杂度。
定义
给定两正值函数\(f\)和\(g\),定义:\(f(n)=\mathcal{O}(g(n))\),条件为:存在正实数\(c\)和\(N\),使得对于所有的\(n \geq N\),有\(|f(n)| \leq |cg(n)| \)
上述的定义表明,当\(n\)足够大,大过一个特定的\(N\)时,且存在一个正数\(c\),使得\(|f|\)不大于\(|cg|\),则\(f\)是\(g\)的\(\mathcal{O}\)表示。\(f\)和\(g\)的关系可以理解为\(g(n)\)是\(f(n)\)的一个上界,也可以理解为\(f\)最终至多增涨的速度与\(g\)一样快,但不会超过\(g\)的增涨速度。
常见复杂度
| 符号 | 名称 |
|---|---|
| \(\mathcal{O}(1)\) | 常数 |
| \(\mathcal{O}(\log{n})\) | 对数 |
| \(\mathcal{O}((\log{n})^c)\) | 多对数 |
| \(\mathcal{O}(n)\) | 线性 |
| \(\mathcal{O}(n\log(n))\) | 线性对数 |
| \(\mathcal{O}(n^2)\) | 平方 |
| \(\mathcal{O}(n^c)\) | 多项式 |
| \(\mathcal{O}(c^n)\) | 指数 |
| \(\mathcal{O}(n!)\) | 阶乘 |
几个关系
大O表示法:
\(f(x) = O(g(x))\) 表示\(f(x)\)以\(g(x)\)为上界。上界并不是确接。例如\(n^2\)的上界可以是\(n^3\)。
实际上\(O(g(x))\)应该是一个函数的集合,所以应该写成\(f(x)∈O(g(x))\)。
小o表示法:
\(f(x) = o(g(x))\)表示\(f(x)\)趋近于\(g(x)\)。例如\(f(x)=x^2+1\), \(g(x)=x^2\)。
Ω表示法:
\(f(x) = Ω(g(x))\)表示\(f(x)\)以\(g(x)\)为下界。例如\(n(g(x))\)是\(n^2(f(x))\)的一个下界。
θ表示法:
\(f(x) = θ(g(x))\)说明\(g(x)\)是\(f(x)\)的确界。也就是同时满足\(f(x) = O(g(x))\)且\(f(x) = Ω(g(x))\)。
二分搜索
在计算机科学中,二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
时间复杂度\(\mathcal{O}(\log n)\), 空间复杂度\(\mathcal{O}(1)\)。
示例代码
// 递归版本
int binary_search(const int arr[], int start, int end, int khey) {
if (start > end)
return -1;
int mid = start + (end - start) / 2; //直接平均可能會溢位,所以用此算法
if (arr[mid] > khey)
return binary_search(arr, start, mid - 1, khey);
if (arr[mid] < khey)
return binary_search(arr, mid + 1, end, khey);
return mid; //最後檢測相等是因為多數搜尋狀況不是大於要不就小於
}
// while循环
int binary_search(const int arr[], int start, int end, int khey) {
int mid;
while (start <= end) {
mid = start + (end - start) / 2; //直接平均可能會溢位,所以用此算法
if (arr[mid] < khey)
start = mid + 1;
else if (arr[mid] > khey)
end = mid - 1;
else
return mid; //最後檢測相等是因為多數搜尋狀況不是大於要不就小於
}
return -1;
}
数学归纳法
数学归纳法(Mathematical Induction、MI、ID)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。
虽然数学归纳法名字中有“归纳”,但是数学归纳法并非不严谨的归纳推理法,它属于完全严谨的演绎推理法。事实上,所有数学证明都是演绎法。
定义
最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。证明分下面两步:
骨牌一个接一个倒下,就如同一个值到下一个值的过程。
证明当n = 1时命题成立。
证明如果在n = m时命题成立,那么可以推导出在n = m+1时命题也成立。(m代表任意自然数)
这种方法的原理在于:首先证明在某个起点值时命题成立,然后证明从一个值到下一个值的过程有效。当这两点都已经证明,那么任意值都可以通过反复使用这个方法推导出来。把这个方法想成多米诺效应也许更容易理解一些。例如:你有一列很长的直立着的多米诺骨牌,如果你可以:证明第一张骨牌会倒。
证明只要任意一张骨牌倒了,那么与其相邻的下一张骨牌也会倒。
那么便可以下结论:所有的骨牌都会倒下。
插入排序
快速排序
归并排序
排序性能
| 算法 | 最差 | 平均 | 空间 |
|---|---|---|---|
| 插入排序 | \(n^2/2\) | \(n^2/4\) | in place |
| 快速排序 | \(n^2/2\) | \(θ(n\log n)\) | 额外的\(\mathcal{O}(\log n)\) |
| 归并排序 | \(n\log n\) | \(θ(n\log n)\) | 额外的\(\mathcal{O}(n)\) |
| 堆排序 | \(2n\log n\) | \(θ(n\log n)\) | in place |
有向图和无向图
数据结构的定义
adjacency list
adjacency matrices
图和树的区别
A tree is a connected graph with no cycles (acyclic).
A non connected graph with no cycles consists of several trees and is called a forest.
A tree with n vertices will always have exactly n-1 edges.
A rooted tree is a tree in which one vertex has been designated as root.
There is exactly one path between any two vertices in G
G is connected and removal of one edge disconnects G
G is acyclic (does not contain cycles) and adding one edge creates a cycle
前缀表达式,后缀表达式
它们都是对表达式的记法,因此也被称为前缀记法、中缀记法和后缀记法。它们之间的区别在于运算符相对与操作数的位置不同:前缀表达式的运算符位于与其相关的操作数之前;中缀和后缀同理。
举例:
(3 + 4) × 5 - 6 就是中缀表达式
- × + 3 4 5 6 前缀表达式
3 4 + 5 × 6 - 后缀表达式
中缀表达式(中缀记法)
中缀表达式是一种通用的算术或逻辑公式表示方法,操作符以中缀形式处于操作数的中间。中缀表达式是人们常用的算术表示方法。
虽然人的大脑很容易理解与分析中缀表达式,但对计算机来说中缀表达式却是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。对计算机来说,计算前缀或后缀表达式的值非常简单。
前缀表达式(前缀记法、波兰式)
前缀表达式的运算符位于操作数之前。
前缀表达式的计算机求值:
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 op 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
例如前缀表达式“- × + 3 4 5 6”:
(1) 从右至左扫描,将6、5、4、3压入堆栈;
(2) 遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素,注意与后缀表达式做比较),计算出3+4的值,得7,再将7入栈;
(3) 接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈;
(4) 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
可以看出,用计算机计算前缀表达式的值是很容易的。
将中缀表达式转换为前缀表达式:
遵循以下步骤:
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从右至左扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
(4-1) 如果S1为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入S1;
(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是右括号“)”,则直接压入S1;
(5-2) 如果是左括号“(”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到右括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最左边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果即为中缀表达式对应的前缀表达式。
例如,将中缀表达式“1+((2+3)×4)-5”转换为前缀表达式的过程如下:
| 扫描到的元素 | S2(栈底->栈顶) | S1 (栈底->栈顶) | 说明 |
|---|---|---|---|
| 5 | 5 | 空 | 数字,直接入栈 |
| - | 5 | - | S1为空,运算符直接入栈 |
| ) | 5 | - ) | 右括号直接入栈 |
| 4 | 5 4 | - ) | 数字直接入栈 |
| × | 5 4 | - ) × | S1栈顶是右括号,直接入栈 |
| ) | 5 4 | - ) × ) | 右括号直接入栈 |
| 3 | 5 4 3 | - ) × ) | 数字 |
| + | 5 4 3 | - ) × ) + | S1栈顶是右括号,直接入栈 |
| 2 | 5 4 3 2 | - ) × ) + | 数字 |
| ( | 5 4 3 2 + | - ) × | 左括号,弹出运算符直至遇到右括号 |
| ( | 5 4 3 2 + × | - | 同上 |
| + | 5 4 3 2 + × | - + | 优先级与-相同,入栈 |
| 1 | 5 4 3 2 + × 1 | - + | 数字 |
| 到达最左端 | 5 4 3 2 + × 1 + - | 空 | S1中剩余的运算符 |
因此结果为“- + 1 × + 2 3 4 5”。
后缀表达式(后缀记法、逆波兰式)
后缀表达式与前缀表达式类似,只是运算符位于操作数之后。
后缀表达式的计算机求值:
与前缀表达式类似,只是顺序是从左至右:
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 op 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
例如后缀表达式“3 4 + 5 × 6 -”:
(1) 从左至右扫描,将3和4压入堆栈;
(2) 遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素,注意与前缀表达式做比较),计算出3+4的值,得7,再将7入栈;
(3) 将5入栈;
(4) 接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
(5) 将6入栈;
(6) 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
将中缀表达式转换为后缀表达式:
与转换为前缀表达式相似,遵循以下步骤:
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从左至右扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
(4-1) 如果S1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的高,也将运算符压入S1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是左括号“(”,则直接压入S1;
(5-2) 如果是右括号“)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最右边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)。
例如,将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下:
| 扫描到的元素 | S2(栈底->栈顶) | S1 (栈底->栈顶) | 说明 |
|---|---|---|---|
| 1 | 1 | 空 | 数字,直接入栈 |
| + | 1 | + | S1为空,运算符直接入栈 |
| ( | 1 | + ( | 左括号,直接入栈 |
| ( | 1 | + ( ( | 同上 |
| 2 | 1 2 | + ( ( | 数字 |
| + | 1 2 | + ( ( + | S1栈顶为左括号,运算符直接入栈 |
| 3 | 1 2 3 | + ( ( + | 数字 |
| ) | 1 2 3 + | + ( | 右括号,弹出运算符直至遇到左括号 |
| × | 1 2 3 + | + ( × | S1栈顶为左括号,运算符直接入栈 |
| 4 | 1 2 3 + 4 | + ( × | 数字 |
| ) | 1 2 3 + 4 × | + | 右括号,弹出运算符直至遇到左括号 |
| - | 1 2 3 + 4 × + | - | -与+优先级相同,因此弹出+,再压入- |
| 5 | 1 2 3 + 4 × + 5 | - | 数字 |
| 到达最右端 | 1 2 3 + 4 × + 5 - | 空 | S1中剩余的运算符 |
因此结果为“1 2 3 + 4 × + 5 -”(注意需要逆序输出)。
编写Java程序将一个中缀表达式转换为前缀表达式和后缀表达式,并计算表达式的值。其中的toPolishNotation()方法将中缀表达式转换为前缀表达式(波兰式)、toReversePolishNotation()方法则用于将中缀表达式转换为后缀表达式(逆波兰式):
深度优先
略。
广度优先
略。
最短路径
Dijkstra
略。
Floyd
略。
KMP算法
https://www.cnblogs.com/zhangtianq/p/5839909.html
http://blog.csdn.net/yutianzuijin/article/details/11954939/
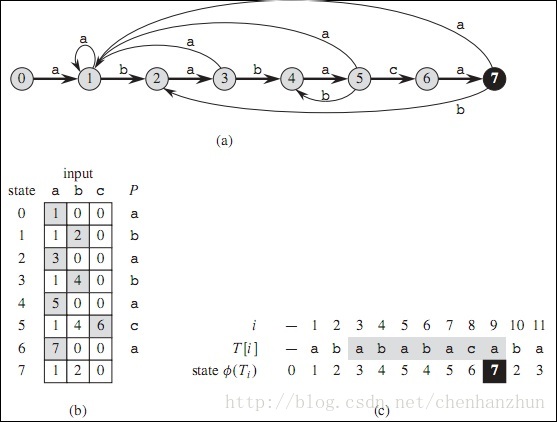
有限自动机匹配字符串
finite automate
有限自动机(Finite Automata)字符串匹配算法最主要的是计算出转移函数。即给定一个当前状态k和一个字符x,计算下一个状态;计算方法为:找出模式pat的最长前缀prefix,同时也是pat[0...k-1]x(注意:字符串下标是从0开始)的后缀,则prefix的长度即为下一个状态。匹配的过程是比较输入文本子串和模式串的状态值,若相等则存在,若不想等则不存在。